Modulare Exponentiation („schnelles Potenzieren“)

Die modulare Exponentiation spielt in der Kryptographie sowie zum ver- als auch zum entschlüsseln von Nachrichten eine wichtige Rolle. Beim RSA-Verfahren z.B. besteht die Chiffrierung in der Berechnung von $m^b \ mod \ n$ .

Verschiedene Möglichkeiten eine Potenzierung duchzuführen:

Eine naive Methode wäre es durch eine Reihe von Multiplikationen
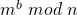$m^b \ mod \ n$ zu berechnen. Demnach wären 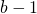$b-1$ Multiplikation notwendig.
Eine weitere Methode wäre das Wiederholte Quadrieren:
$m^{16} = ( ( ( a^2 ) ^2 ) ^2 ) ^2$
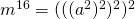
Ein effizienteres Potenzieren kann auch wie folgt durchgeführt werden:
$m^{26} = m^{16} \cdot m^8 \cdot m^2$
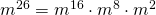
Ein gutes Rezept für ein schnelles Potenzieren ist für ein allgemeines 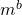$m^b \$ b ins Binärsystem zu überführen: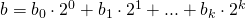
$b = b_0 \cdot 2^0 + b_1 \cdot 2^1 + ... + b_k \cdot 2^k \$
anschließend berechnet man wiederholt Quadrate von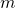 $m$ , dies erzeugt nacheinander: 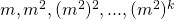$m, m^2, (m^2)^2, ..., (m^2)^k \$ und multipliziert ein 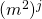$(m^2)^j$ zum Endergebnis wenn 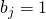$b_j = 1$ . Daraus ergibt sich eine höchste Anzahl an Multiplikationen von $2 \cdot \lceil log_2(b) \rceil$ .

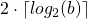Programmbeispiel der modularen Exponentiation

Es gilt z.Bsp.:
$m^{23}=m^{22} \cdot m$

daraus folgt für $m^{22}$ :
$m^{22}=(m^{11})^2$

Rekursiv kann die modularen Exponentiation wie folgt für $m^b$ mit $b \in \mathbb{N}_0$ beschrieben werden:

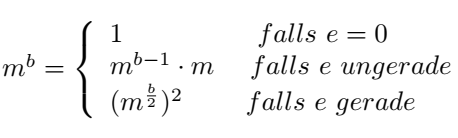
Eine rekursive Implementierung der obigen Rekursionsformeln mit $m=2, \ b=4, \ n=5$ in Python mit dem Rückgabewert als Ergebnis 1:

def modexp(m, b, n):
    if b == 0:
        return 1
    if b % 2==1:
        return modexp(m, b-1, n)*m % n
    else:
        return modexp(m, b//2, n)**2 % n
    
if __name__ == '__main__':
    print(modexp(2,4,5))

Eine iterative Implementierung von $m^b \ mod \ n$ in Python nach der „naiven Methode“ sieht wie folgt aus:

def modexpIt(m, b, n):
    bs=1
    while(b > 0):
        bs *= m
        b -= 1
    erg = bs % n
    return erg
    
if __name__ == '__main__':
    print(modexpIt(2,4,5))

Das obige Beispiel verdeutlicht nocheinmal, dass für die Berechnung von $m^b \ mod \ n$ b-1 Multiplikation bzw. b-1 Schleifendurchläufe notwendig sind.
Bezugnehmend auf das Laufzeitverhalten der Iterativen Implementierung zur Berechnung von $m^b \ mod \ n$ kann man somit sagen, dass diese $O(c)$ (für $c=b-1$ ) beträgt $\Longrightarrow$ lineares Laufzeitverhalten.

Binäres Potenzieren

Das binäre Potenzieren ist eine effizientere Methode für die Exponentation, als die zuvor beschriebenen Verfahren. Sie funktioniert wie folgt:

Für $a^b$ wobei $a,b \in \mathbb{Z}$ wird $b$ binär dargestellt. Für jede 1 wird nun die Operation quadrieren und multiplizieren (QM) und für jede 0 die Operation quadrieren (Q) durchgeführt. Wobei die führende 1 gestrichen werden kann, da die Binärdarstellung für $b>0$ immer mit einer 1 beginnt und damit auch die erste Anweisung mit QM, ergibt sich hierfür $1^2 \cdot a = 1$ .

Beispiel:

für $a=5$ und $b=13 \Longrightarrow 5^{13}$ .

$b_2 \ (dual) \ =1101$ die führende 1 wird nun gestrichen $\Longrightarrow$ 101. Nun werden für $a$ folgende Operationen durchgeführt:

QM $\longrightarrow$ Q $\longrightarrow$ QM

Für $a$ ergibt sich nun:

$a^2 \cdot a \longrightarrow$ QM
$(a^2 \cdot a)^2 \longrightarrow$ Q
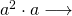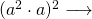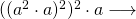$((a^2 \cdot a)^2)^2 \cdot a \longrightarrow$ QM

Kongret für $a=5$ erhält man:

$((5^2 \cdot 5)^2)^2 \cdot 5 = 1220703125$

In der Programmiersprache Python lässt sich das Ganze wie folgt beschreiben:

'''Umwandlung in binaer und Ergebnis als Liste zurueckliefern'''
def sammleBin(exponent):
    binListe = []
    tmpgerade = 0
    if exponent % 2 == 0:
        tmpgerade = exponent
        exponent = exponent + 1
    while exponent != 0:
        binListe.insert(0,exponent % 2)
        exponent = exponent // 2
    if tmpgerade != 0:
        binListe[len(binListe)-1] = 0
    '''erstes Element aus Liste entfernen'''
    del binListe[0]
    return binListe

'''Entsprechende Operationen durchfuehren (QM oder Q)'''
def binPotenz(basis, expo):
    binListe = sammleBin(expo).copy()
    wert = basis
    for i in range(0, len(binListe)):
        if(binListe[i] == 1):
            wert = basis * (wert**2)
        else:
            wert = wert**2
    return wert

if __name__ == '__main__':
    print("",binPotenz(5, 13))

Nähere Informationen über die Binäre Exponentiation findet man bei Wikipedia.

IT-Sicherheit

IT- und Systemsicherheit

Modulare Exponentiation („schnelles Potenzieren“)

Programmbeispiel der modularen Exponentiation

Binäres Potenzieren

Schreibe einen Kommentar Antworten abbrechen