Unter einer Primzahl versteht man eine von 1 verschiedene natürliche Zahl, die nur durch 1 und durch sich selbst teilbar ist.
Die Menge der Primzahlen wird in der Regel mit dem Symbol ![]() bezeichnet. Mit
bezeichnet. Mit ![]() verknüpft ist die Folge
verknüpft ist die Folge ![]() der nach ihrer Größe geordneten Primzahlen, die man auch Primzahlfolge nennt.
der nach ihrer Größe geordneten Primzahlen, die man auch Primzahlfolge nennt.
Demanch gilt:
![]()
Da wir nun festgelegt haben, was eine Primzahl ist, stellt sich nun die
Frage, wofür werden diese in der Kryptographie verwendet und warum haben
diese einen so großen Stellenwert inne?
In der Kryptographie basieren viele Verschlüsselungsverfahren auf Primzahlen, so z.B. das RSA (Rivest-Shamir-Adleman)-Verfahren.
Beispiel einer verschlüsselten Übertragung anhand des RSA-Verfahrens:
Die Personen Alice und Bob möchten verschlüsselt kommunizieren. Zuerst möchte Bob Alice eine geheime Nachricht schicken. Um dies zu ermöglichen, trifft Alice folgende Vorbereitungen:
1) Alice wählt zufällig zwei Primzahlen 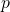 und
und 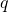 .
2) Sie berechnet
.
2) Sie berechnet 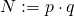 und
und 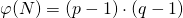 .
3) Dann wählt Sie
.
3) Dann wählt Sie 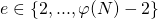 mit
mit 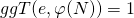 .
4) Alice bestimmt
.
4) Alice bestimmt 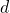 mit
mit 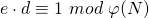 .
5) Dann ist
.
5) Dann ist 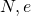 der öffentliche und
der öffentliche und 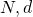 der geheime Schlüssel.
6) Die Werte
der geheime Schlüssel.
6) Die Werte 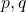 und
und 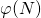 löscht Alice.
löscht Alice.Bob möchte nun Alice die Nachricht ![]() schicken. Er geht nun wie folgt vor:
schicken. Er geht nun wie folgt vor:
7) Bob berechnet 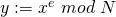 und schickt
und schickt 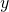 an Alice.
8) Alice berechnet
an Alice.
8) Alice berechnet 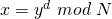 .
.Es stellen sich nun z.B folgende Fragen:
- Wie findet man ausreichend große Primzahlen
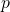 und
und 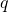 ?
? - Was bedeutet die Funktion
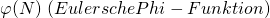 ?
? - Wie wird die Rechenoperation
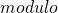 (Division mit Rest) angewendet ?
(Division mit Rest) angewendet ?
Auf diese Fragen wird in Beiträgen in den Kategorien Zahlentheorie und Primzahltest noch näher eingegangen.
