Sowohl im Ring der ganzen Zahlen (ganze Zahlen können ohne Einschränkung addiert, subtrahiert und multipliziert werden) als auch im Polynomring über einem Körper kann stets die Division mit Rest (euklidischer Ring) durchgeführt werden.
Formaler Algorithmus:
Seien 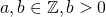 .
1) Berechne den ganzzahligen Quotienten
.
1) Berechne den ganzzahligen Quotienten 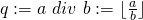 von
von  und
und 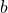 .
2) Berechne den Rest
.
2) Berechne den Rest 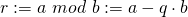 .
3) Gebe
.
3) Gebe 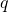 und
und  aus.
Dann gilt:
aus.
Dann gilt: 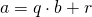 mit
mit  .
.Beispiele:
