Laut Wikipedia sind zwei Zahlen ![]() und
und ![]() kongruent
kongruent ![]() , wenn sie bei der Division durch
, wenn sie bei der Division durch ![]() denselben Rest haben. Dies ist genau dann der Fall, wenn sie sich um ein ganzahliges Vielfaches von
denselben Rest haben. Dies ist genau dann der Fall, wenn sie sich um ein ganzahliges Vielfaches von ![]() unterscheiden.
unterscheiden.
Stimmen die Reste nicht überein, so nennt man die Zahlen inkongruent ![]() . Jede Kongruenz modulo einer ganzen Zahl ist eine Kongruenz auf dem Ring der ganzen Zahlen.
. Jede Kongruenz modulo einer ganzen Zahl ist eine Kongruenz auf dem Ring der ganzen Zahlen.
Verdeutlicht wird dies anhand folgender Beispiele:
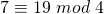 ; da
; da 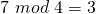 und
und 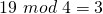 ist.
ist.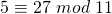 ; da
; da 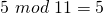 und
und 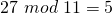 ist.
ist. 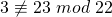 ; da
; da 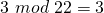 und
und 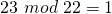 ist.
ist.
Ein einfaches Python-Programm zum bestimmen der Kongruenz zweier Zahlen ![]() und
und ![]() modulo
modulo ![]() für
für ![]() kann wie folgt implementiert werden:
kann wie folgt implementiert werden:
def isKongruent(a, b, m):
restA = a % m
restB = b % m
if restA == restB:
return True
else:
return False
if __name__ == '__main__':
print("Sind a und b kongruent mod m?", isKongruent(7, 19, 4))Obiges Programm liefert als Wahrheitswert True da ![]() ist.
ist.
