Der Euklidische Algorithmus
Der Euklidische Algorithmus dient dazu, den größten gemeinsamen Teiler (
) zweier natürlicher Zahlen zu ermitteln. Das Ermitteln des findet in der Kryptographie bei vielen Kryptosystemen Anwendung.
Beispiel:
Es soll für zwei natürliche Zahlen 
und 
der 
ermittelt werden.
Formal kann die Ausgangssituation wie folgt beschrieben werden: 
(
steht hierbei für den Rest der ganzahligen Division).
Beispiel für und :
In der letzten Zeile kann der 
abgelesen werden (fett gedruckte 3). Die Berechnung des ist abgeschlossen, sobald der Rest (r) den Wert 0 angenommen hat.
Kompakter kann der 
auch in Form einer Tabelle ermittelt werden:
| a | b | r |
| 285 | 33 | 21 |
| 33 | 21 | 12 |
| 21 | 12 | 9 |
| 12 | 9 | 3 |
| 9 | 3 | 0 |
Die Spalte b in der letzten Zeile liefert das Ergebnis .
Als Python-Programm lässt sich die Ermittlung des wie folgt implementieren:
def ggt(a ,b):
while b!=0:
a ,b = b, a % b
return a
if __name__ == '__main__':
a = 285
b = 33
print("Ausgabe ggt: ", ggt(a, b))Der erweiterte Euklidische Algorithmus
Der erweiterte Euklidische Algorithmus wird u. a. dazu verwendet lineare diophantische Gleichungen der Form 
zu lösen. Vielfache des 
sind ebenfalls lösbar und können allgemein mit 
für 
beschrieben werden.
Beispiel:
Gegeben sei die lineare diophantische Gleichung: 
Zuerst wir der Euklidische Algorithmus wie zuvor durchgeführt:
Die Werte werden nun in eine Tabelle übertrage. Diese Tabelle erhält neben den Spalten für 
und noch zusätzlich die Spalten für die Werte 
und 
. Die Spalte r spielt bei der Berechnung von 
und keine Rolle und kann auch weggelassen werden.
| a | b | q | r | x | y |
| 285 | 81 | 3 | 42 | 2 |  |
| 81 | 42 | 1 | 39 | -1 |  |
| 42 | 39 | 1 | 3 | 1 |  |
| 39 | 13 | 3 | 0 | 0 |  |
| 13 | 0 | 1 | 0 |
Hierbei gilt für die Berechnungen der Werte für die Spalten und :
- in die letzte Zeile wird immer für
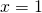und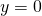 
eingetragen und - anschließend wird sich sukzessive Zeile für Zeile nach oben gearbeit, wobei gilt:
Als Lösung für das obige Beispiel gilt demnach:
Probe: 
In Python lassen sich die Werte für und sowie der 
wie folgt ermitteln:
def extgcd(a, b):
x, y, xi, yi = 1, 0, 0, 1
while b!=0:
q=a//b
a, b = b, a-q*b
y, yi = yi, y-q*yi
x, xi = xi, x-q*xi
return a, x, y
if __name__ == '__main__':
print("Werte a, x, y: ", extgcd(285, 81))