Die Eulersche -Funktion gibt für jede natürliche Zahl an, wie viele zu teilerfremde natürliche Zahlen es gibt, die nicht größer als sind.

Definition:

Sei :
Die Eulersche -Funktion ist dann definiert durch:
dabei bezeichnet den größten gemeinsamen Teiler von .

Beispiele:

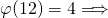• denn in der Menge 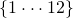sind nur die Zahlen 1, 5, 7, 11 teilerfremd.
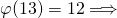• da 13 eine Primzahl ist, sind alle Zahlen die kleiner sind als 13 teilerfremd.
  

Es lassen sich nun folgende Aussagen treffen:

1) Für jede Primzahl gilt: .
2) Sei eine Primzahl und . Dann gilt:

Beispiel zu 2):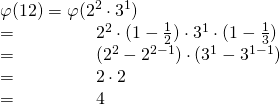

In Python lässt sich die Berechnung von relativ einfach wie folgt implementieren:

def calcphi(phivonN):
    i = 1
    wertPhi = 0
    while i < phivonN:
        if testggT(i, phivonN) == 1:
            wertPhi += 1
        i += 1
    return wertPhi

def testggT(i, phivonN):
    while phivonN!=0:
        i ,phivonN = phivonN, i % phivonN
    return i

if __name__ == '__main__':
    phivonN = 12
    print("Phi(",phivonN,")", "= ", calcphi(phivonN))