In der Kryptographie wird zwischen symmetrischen und asymmetrischen Kryptosystemen unterschieden. Diese unterscheiden sich vorallem in der Anzahl der verwendeten Schlüssel.

symmetrische Verschlüsselung

Beim symmetrischen Kryptoverfahren gibt es, anders als beim asymmetrischen Kryptoverfahren, nur einen Schlüssel. Dieser Schlüssel dient sowohl zur Ver- als auch zur Entschlüsselung. Dies bedeutet, falls Informationen ausgetauscht werden sollen, dass sowohl der Sender als auch der Empfänger im Besitz des Schlüssels sein müssen. Beim Sender ist dies natürlich kein Problem, da er bereits im Besitz des Schlüssels ist.

Beim Empfänger jedoch stellt sich die Frage, auf welchem Übertragungsweg der Schlüssel (Passwort, Key, …) sicher mitgeteilt oder übergeben werden kann. Dies ist auch zugleich ein Hauptnachteil der symmetrischen Verschlüsselung.

Beachtet werde muss, dass man symmetrische Kryptoverfahren in Block- und Stromchiffren unterteilen kann. Bei Stromchiffren wird z.B. der Klartext Zeiche für Zeichen verschlüsselt, während der Geheimtext auch wieder Zeichen für Zeichen entschlüsselt werden muss. Hingegen bei Blockchiffren, werden die Zeichen des Textes in feste Blockgrößen eingeteilt, sodass mehrere Zeichen in einem Schritt ver- bzw. entschlüsselt werden können.

Vorteile der symmetrischen Verschlüsselung sind:

• einfaches Schlüsselmanagement, da nur ein Schlüssel zum ver- und entschlüsseln benötigt wird
• verhältnismäßig hohe Geschwindigkeit für Ver- und Entschlüsselung, da Verfahren meist auf effizienten Operationen wie Bit-Shifts und logischen XOR-Operationen aufbauen
  

Nachteile der symmetrischen Verschlüsselung sind:

• nur ein Schlüssel zur Ver- und Entschlüsselung, dieser darf nicht in unbefugte Hände geraten
• wie schon erwähnt, muss der Schlüssel über einen sicheren Kommunikationskanal ausgetauscht werden
• Anzahl der Schlüssel bezogen auf die Anzahl der Teilnehmer wächst quadratisch
  

Symmetrische Kryptoverfahren:

• AES – Advanced Encryption Standard
• DES – Data Encryption Standard (Schlüssellänge nur 56-Bit für mache Anwendungen nicht ausreichend sicher)
• Trible DES – auch als TDES, 3DES oder DESede bezeichnet
• IDEA – International Data Encryption Algorithm
• Blowfish
• Towfish
• CAST-128, CAST-256
• RC2, RC4, RC5, RC6
• Fox
  

asymmetrische Verschlüsselung

Bei einem asymmetrischen Kryptosystem arbeitet man, anders als beim symmetrischen Kryptosystem, mit zwei unterschiedlichen Schlüsseln. Ein Schlüssel, der sogenannte Public Key, dient der reinen Verschlüsselung. Der zweite Schlüssel, der Private Key, dient der Entschlüsselung und sollte vom Eigentümer gut und sicher aufbewahrt werden.

Dieses Schlüsselpaar, der Public Key und der Private Key, hängt über einen mathematischen Algorithmus eng zusammen. Daten die mit dem öffentlichen Schlüssel verschlüsselt wurden, können nur mit dem privatem Schlüssel wieder entschlüsselt werden (siehe Abbildung unten). Der private Schlüssel muss daher vom Besitzer geheim gehalten werden.

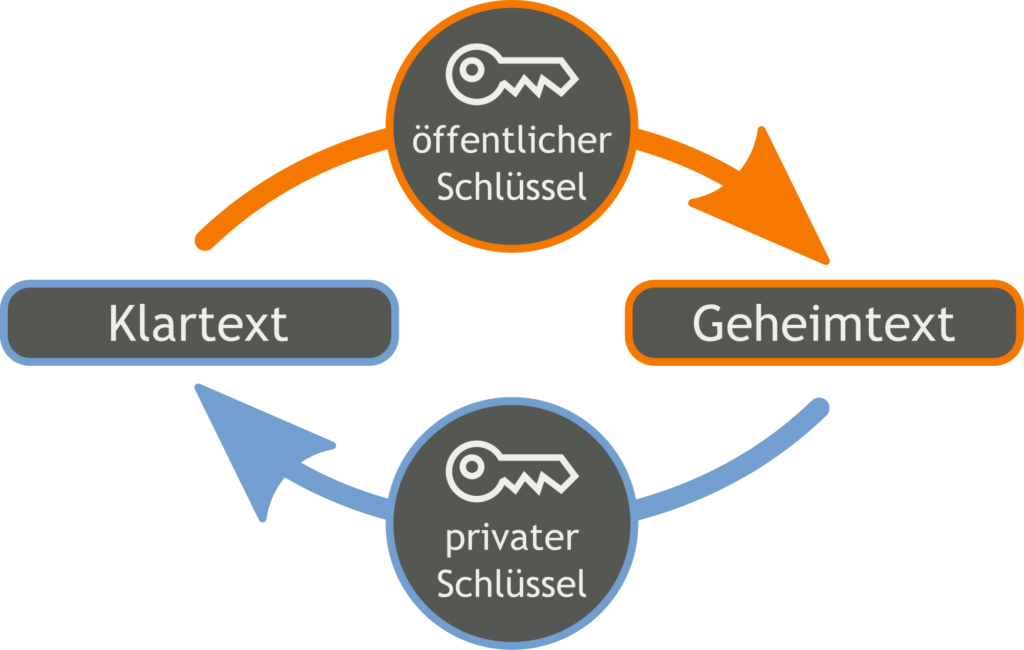
Ein konkreter Anwendungsfall könnte z. B. wie folgt aussehen: Will Benutzer A Daten verschlüsselt an Benutzer B übermitteln, so muss er ihm seinen öffentlichen Schlüssel übermitteln. Der private Schlüssel hingegen bleibt im Besitz von Benutzer A. Benutzer B verschlüsselt nun die Nachricht mit dem Public Key von Benutzer A und kann nun die geheime Nachricht an Benutzer A senden. Benutzer A kann nun wiederum die geheime Nachricht mit Hilfe seines privaten Schlüssels wieder entschlüsseln

Das Problem der asymmetrischen Verschlüsselung ist die Verteilung des Public Keys. In der Regel gesschieht die beim Erstkontakt mit dem Kommunikationspartner. Jedoch stellt sich hierbei die Frage, ob der vermutete Kommunikationspartner auch derjenige ist, für den er sich ausgibt.

Bei Asymmetrische Kryptosysteme geht es in der Regel darum, eine Funktion zu wählen, die sehr einfach zu berechenen ist, deren Umkehrung hingegen sich als sehr aufwendig gestaltet. Realisiert wird dies mit Modulo-Rechenfunktionen (siehe Kategorie Zahlentheorie). Diese sind teilweise recht einfach zu berechenen, jedoch gestaltet sich deren Umkehrung als sehr aufwendig. Solche Funktionen bezeichnet man auch als Einwegfunktionen. Funktionen bei denen sich die Umkehrung mit einer zusätzlichen Information abkürzen lässt, werden als Falltürfunktionen bezeichnet.

Ein Beispiel für eine Einwegfunktion ist der diskrete Logarithmus. Dieser kann sehr leicht berechnet werden. Umgekehrt ist es jedoch nicht in praktikabler Zeit möglich eine große Zahl zurüchzurechnen. Man bezeichnet dies als Diskreter-Logarithmus-Problem. Viele asymmetrische Verschlüsselungsverfahren beruhen darauf. Allerdings soll dies nicht bedeuten, dass nicht irgendwann ein Weg gefunden wird das Diskrete-Logarithmus-Problem zu lösen.

Beispiel:

Der diskrete Logarithmus beschreibt eine Kongruenz der Form: wobei geheim ist.






lässt sich nur durch probieren ermitteln.

Untenstehender Python-Code liefert das erste Ergebnis durch einfaches probieren für den Wert . Im Beispiel wird der Wert für schnell ermittelt, da die einzelnen Werte relativ klein gewählt wurden.

'''Phython-Programm zur Ermittlung von x'''
def calcX(a, m, p):
    i = 1
    while ((a**i % p) != (m % p)):
        i += 1
    return i
        
if __name__ == '__main__':
    a = 2
    m = 396923
    p = 1419403
    '''Berechnet a^i kongruent m modulo p'''
    diskLog = calcX(a, m, p)
    print("Wert fuer diskreten Logarithmus: ", diskLog)

Eine weitere Einwegfunktion ist das Multiplizieren von Primzahlen. Während die Multiplikationen für einen Computer kein Problem darstellt, so ist das Zurückrechnen d. h. das Zerlegen des Primzahlproduktes in die einzelnen Primfaktoren, bei sehr großen Primzahlen nicht in praktikabler Zeit möglich. Man spricht hierbei von Faktorisierung und in dem Zusammenhang vom Faktorisierungsproblem.

Beispiel:

Man berechnet . Als Ergebnis erhält man 713. Um nun die 713 wieder in ihre einzelnen Faktoren zu zerlegen, gibt es hier nur einen Weg; man muss alle Möglichkeiten durchprobieren. Sind die Primzahlen sehr groß gewählt, so dauert dies sehr sehr lange.

Untenstehendes Pythonprogramm liefert einen möglichen Algorithmus zur Primfaktorzerlegung.

'''Python-Programm zur Primfaktorzerlegung'''
def primfaktor(zahl):
    primListe = []
    while zahl % 2 == 0:
        primListe.append(2)
        zahl = zahl // 2
    i = 2
    while i <=  zahl:
        if zahl % i == 0:
            primListe.append(i)
            zahl = zahl // i
            i = 2
        i += 1
    primListe.append(zahl)
    primListe.sort()
    if primListe[0] == 1:
        primListe.remove(1)
    return primListe  
    
if __name__ == '__main__':
    zahl = 713
    print(primfaktor(zahl))

Mögliche Angriffe auf asymmetrische Verschlüsselungsverfahren:

• Public-Key-Only-Angriff: Ist der öffentliche Schlüssel bekannt, kann der Angreifer beliebigen Klartext verschlüsseln und beispielsweise mit bereits verschlüsselten Klartext vergleichen.
• Chosen-Cipertext-Angriff: Der Angreifer schickt einen beliebigen Geheimtext an sein Ziel, um diesen entschlüsseln zu lassen.

Asymmetrische Kryptoverfahren:

Die bekanntesten asymmetrischen Kryptoverfahren sind das RSA- und das Diffie-Hellmann-Verfahren.

• Diffie-Hellmann-Merkle-Schlüsselaustausch
• RSA: Rivest, Shamir und Adelman
• MQV: Menezes, Qu und Vanstone (LMQSV)
• PGP: Pretty Good Privacy (OpenPGP)