Unter Reverse Engineering versteht man das Zurückführen des vorliegenden Binärcodes zum dem eigentliche Quellcode. Es kann auch dazu verwendet werden um Informationen aus dem compilierten Quellcode zu erlangen, bzw. diesen teilweise zu manipulieren.

In der Regel geschieht dies mit unterschiedlichen Debuggern (z. B.: x96dbg). Hier werden dann die verschiedenen CPU-Operationen im Assembler-Code dargestellt. Mit Hilfe dieser einzelnen Assembler-Ausführungsroutinen können Rückschlüsse auf unterschiedliche Informationen innerhalb der Software(Software-Keys, Erlangen von Passwörter, Erstellen von Keylogger, Umwandlung von Shareware-Versionen in Vollversionen usw.) gezogen werden.

Beispiele wie ein solches Reverse Engineering durchgeführt werden kann, wird anschließend anhand von .class-Dateien und .exe-Dateien noch näher erläutert.

Ich muss noch darauf hinweisen, das die hier beschriebenen Methoden nicht für illegale Zwecke missbraucht werden dürfen. Diese dienen rein experimentellen Vorhaben. Der Leser dieser Beiträge verpflichtet sich, sich keinen unberechtigten Zugang zu kostenpflichtiger Software zu verschaffen.

Für die kommenden zwei Beispiele wird zum einen eine .class-Java-Datei und zum anderen eine .exe-C#-Datei für ein Reverse Engineering verwendet. In beiden Programmen ist das jeweilige Passwort, dass für einen Simulierten Zugang verwendet werden soll, fest und unverschlüsselt im Programmcode enthalten. Man sollte nicht dem Druckschluss unterliegen und Glauben, da nur der Byte- bzw. der Binär-Code vorliegt das Passwort nicht auslesbar wäre. Passwörter sollten immer verschlüsselt abgelegt werden (siehe Beispiel „Passwort Hashing mit BCrypt“).

Reverse Engineering am Beispiel einer Java-.class-Datei

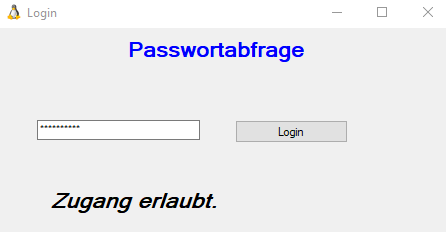
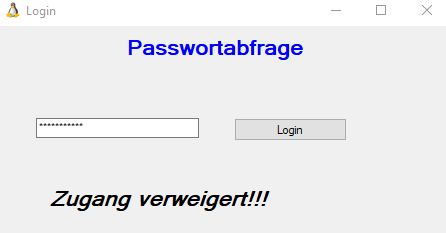
Als Beispiel wird nun eine einfaches JavaFX-Programm genommen, das die Eingabe eines Benutzers mittels Passwort überprüft. Ist die Eingabe korrekt, wird als Ergebnis „Zugang erlaubt.“ ausgegeben, ansonsten „Zugang verweigert!!!“.

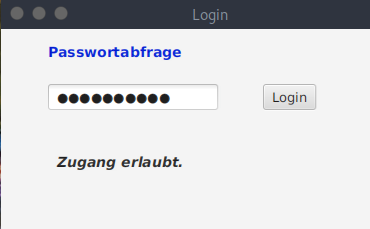
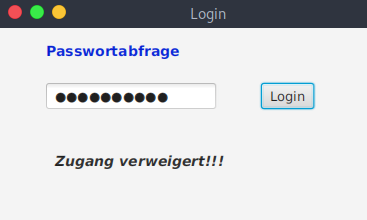
Die interessante Klasse des Programm-Codes ist PassController, da hier das Passwort festgelegt wird (s.u.).

package reverseEng;

import javafx.event.ActionEvent;
import javafx.fxml.FXML;
import javafx.scene.control.Button;
import javafx.scene.control.Label;
import javafx.scene.control.PasswordField;

public class PassController
{
	@FXML
	private PasswordField myPasswordField;
	@FXML
	private Button checkPassButton;
	@FXML
	private Label meldung;	

	// naive Methode: Passwort liegt unverschluesselt vor.
	private final String MY_SECRET_PASSWORD = "Top@Secret";
	private String aktEingabe;	

	public PassController() 
	{
		// TODO Auto-generated constructor stub
		aktEingabe = "";
	}

	
	public String getAktEingabe()
	{
		return aktEingabe;
	}

	public void setAktEingabe(String aktEingabe)
	{
		this.aktEingabe = aktEingabe;
	}

	
	public String getMySecretPassword()
	{
		return mySecretPassword;
	}

	
	@FXML
	public void checkMyPassword(ActionEvent evt)
	{
		aktEingabe = myPasswordField.getText();

		if(aktEingabe.equals(MY_SECRET_PASSWORD))
		{
			meldung.setText("Zugang erlaubt.");
		}
		else
		{
			meldung.setText("Zugang verweigert!!!");
		}
	}
}

Unser kleines Testprogramm besteht aus drei Dateien: MainLogin.class (Hauptprogramm), PassController.class (Controller-Klasse) und der PassWindow.fxml (dient im wesentliche zur Formatierung).

Da uns in unserem Szenario nur der Byte-Code vorliegt, werden wir diesen mit dem kleinen Programm JD-Gui, einem Java Decompiler, der kostenlos heruntergeladen werden kann, wieder zurück in den eigentliche Quellcode überführen. Wir schauen uns nun die Datei PassController.class mit JD-Gui an.

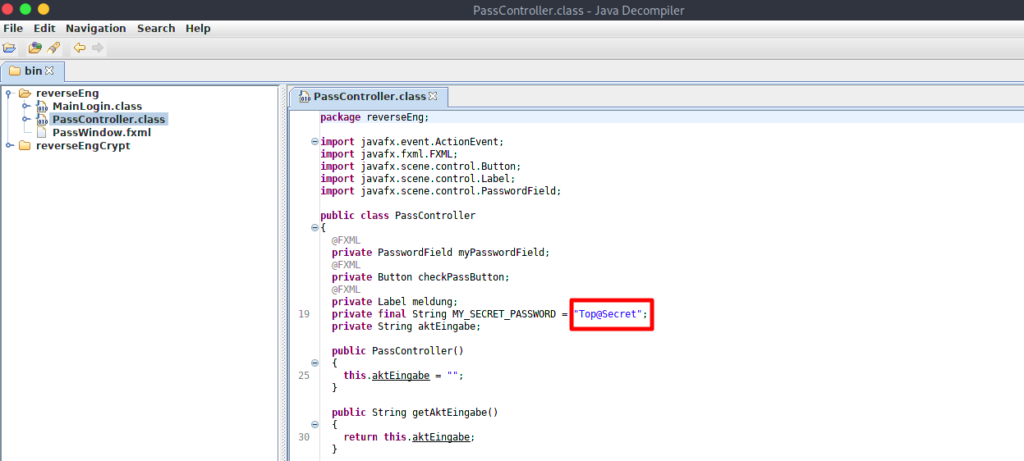
Wie wir feststellen können, kann in JD-Gui das Passwort „Top@Secret“ sehr leicht ausgelesen werden. Class-Java-Dateien können also sehr leicht wieder in den eigentlichen Quellcode überführt werden. Es ist daher keine gute Idee Passwörter im Quellcode unverschlüsselt zu hinterlegen, mit der Annahme es wird schließlich nur der Binärcode weitergegeben und hier könnte das Passwort nicht rekonstruiert werden.

Reverse Engineering am Beispiel einer C#-.EXE-Datei

Wie man bereits im vorherigen Beispiel sehen konnte, ist es sehr einfach Java-Byte-Code wieder in den ursprünglichen Quellcode zu überführen. Passwörter lassen sich allerdings auch aus EXE-Dateien auslesen (im Beispiel PassDeCrypt.exe). Hierzu benutzen wir das vorangegangene Beispiel nur diesmal geschrieben in C# und anschließend kompiliert, damit wir eine EXE-Datei erhalten.

Der C#-Code sieht in unserem Beispiel wie folgt aus:

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace PassDeCrypt
{
    public partial class PassDeCrypt : Form
    {
        private const String MY_SECRET_PASSWORD = "Top@Secret";
        private String eingabe;

        public PassDeCrypt()
        {
            InitializeComponent();
            txt_password.PasswordChar = '*';
            eingabe = "";
        }


        public void SetEingabe(String myEingabe)
        {
            eingabe = myEingabe;
        }


        private void CheckPassword()
        {
            if (MY_SECRET_PASSWORD.Equals(txt_password.Text))
            {
                lb_status.Text = "Zugang erlaubt.";
            }
            else
            {
                lb_status.Text = "Zugang verweigert!!!";
            }
        }


        private void Txt_password_TextChanged(object sender, KeyEventArgs e)
        {
            if(e.KeyCode == Keys.Enter)
            {
                CheckPassword();
            }
        }


        private void Bt_login(object sender, EventArgs e)
        {
            CheckPassword();
        }
    }
}

Auch hier liegt das Passwort innerhalb des Quelltextes im Klartext vor.

Mit Hilfe des Decompilierungstools dnSpy, das ebenfalls kostenlos aus dem Internet heruntergeladen werden kann, lässt sich das im Quellcode enthaltenen Passwort relativ einfach auslesen.

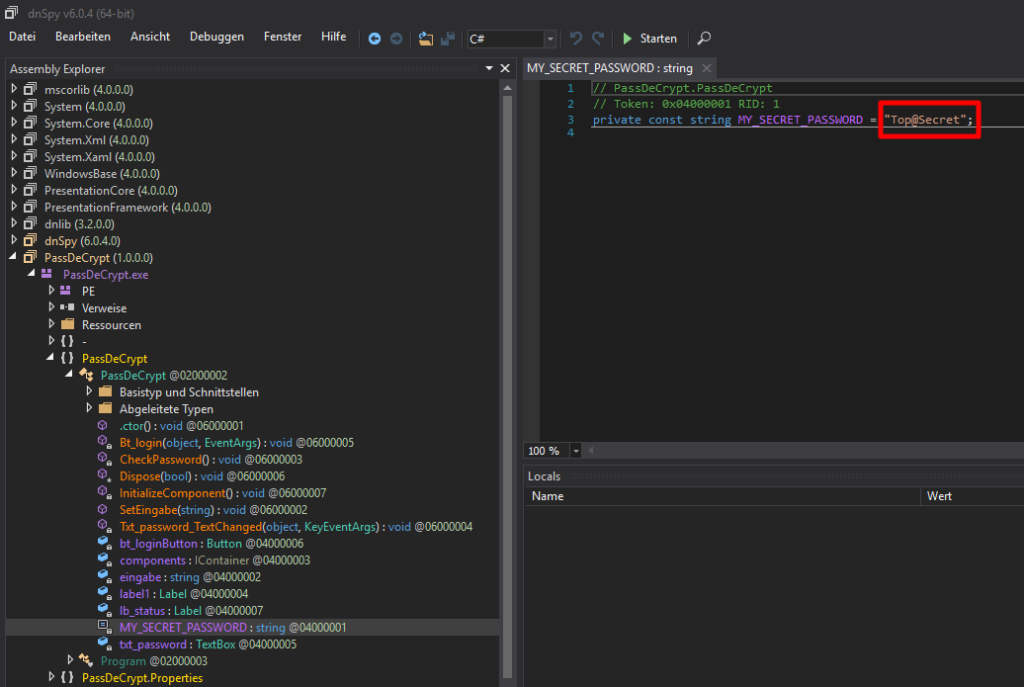
Passwort Hashing innerhalb des Programm-Codes (Java)

Wie wir bereits in vorangegangenen Beispielen gesehen haben, ist es keine besonders gute Idee, ein Passwort im Klartext innerhalb des Programmcodes zu hinterlegen. Es stellt sich nun die Frage, wie geht es besser?

Werden Passwörter hinterlegt, ob innerhalb des Programmcodes oder in einer Datenbank, so sollten dies immer in gehashter Form geschehen. Im folgenden Beispiel wird unser Passwort ‚Top@Secret‘ mit BCrypt gehasht hinterlegt.

Bei BCrypt handelt es sich um eine kryptologische Hashfunktion, die speziell für das Hashen und Speichern von Passwörtern entwickelt wurde. Die auf dem Blowfish-Algorithmus basierende Funktion wurde von Niels Provos und David Mazières konzipiert und auf der USENIX-Konferenz im Jahre 1999 der Öffentlichkeit präsentiert. (Quelle und weitere Informationen: Wikipedia BCrypt).

Nun zum Beispiel; unsere Klasse PassController sieht nun wie folgt aus:

package reverseEngCrypt;

import javafx.event.ActionEvent;
import javafx.fxml.FXML;
import javafx.scene.control.Button;
import javafx.scene.control.Label;
import javafx.scene.control.PasswordField;

public class PassController
{
	@FXML
	private PasswordField myPasswordField;
	@FXML
	private Button checkPassButton;
	@FXML
	private Label meldung;
	
	// Passwort als Passwort-Hash (BCrypt) hinterlegen
	private final String MY_SECRET_PASSWORD = "$2a$07$1tXygQHPJvEdPFMqi.r8BuH/pC5LrrFs5.kVJRANSLlQSUJ9V0TIS";
	
	private String aktEingabe;
	
	public PassController() 
	{
		// TODO Auto-generated constructor stub
		aktEingabe = "";
	}
	
	public String getAktEingabe()
	{
		return aktEingabe;
	}
	
	public void setAktEingabe(String aktEingabe)
	{
		this.aktEingabe = aktEingabe;
	}
	
	public String getMySecretPassword()
	{
		return MY_SECRET_PASSWORD;
	}
	
	@FXML
	public void checkMyPassword(ActionEvent evt)
	{
		aktEingabe = myPasswordField.getText();
		CompareHashes hash = new CompareHashes(MY_SECRET_PASSWORD, aktEingabe);
		
		if(hash.comparePassword())
		{
			meldung.setText("Zugang erlaubt.");
		}
		else
		{
			meldung.setText("Zugang verweigert!!!");
		}
	}
}

Wie man sehen kann ist das Passwort im obigen Beispiel gehasht hinterlegt. Um einen Passwort Abgleich herzustellen benötigt man noch eine zweite Klasse CompareHashes. Die obige Klasse erhält eine Referenz auf diese Klasse um dort den Passwortabgleich über die Funktion comparePassword() herzustellen. Der Konstruktor erhält als Parameter den Passwort-Hash und die Benutzereingabe mit der der Vergleich durchgeführt wird.

package reverseEngCrypt;

import org.springframework.security.crypto.bcrypt.BCryptPasswordEncoder;

public class CompareHashes
{	
	private String hash;
	private String eingabe;
	private BCryptPasswordEncoder encoder;
	
	public CompareHashes(String hash, String eingabe)
	{
		this.hash = hash;
		this.eingabe = eingabe;
		encoder = new BCryptPasswordEncoder();
	}
	
	public boolean comparePassword()
	{
		boolean test = encoder.matches(eingabe, hash);
		return test;
	}
}

Passwörter sollten immer gehasht im Programmcode oder in Datenbanken hinterlegt werden, damit diese nicht mit Hilfe von Debuggern oder anderen Tools ausgelesen werden können.