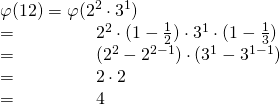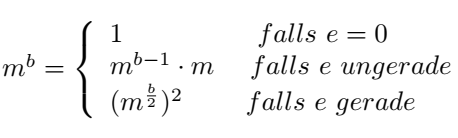Miller-Rabin-Test

Veröffentlicht am 21. November 2018 von juergen

Der Miller-Rabin-Test ist eine Verschärfung des Fermat-Tests und dient ebenfalls der Bestimmung von Primzahlen ( $p$ ). Dieser hat allerdings im Vergleich zum Fermat-Test eine wesentlich höhere Trefferwahrscheinlichkeit in Bezug auf die Bestimmung von Primzahlen.
Beim Miller-Rabin-Test handelt es sich um einen probilistischen Primzahltest. Dies bedeutet, dass die Basis $n$ auf welcher die Exponentation durchgeführt wird zufällig innerhalb des Intervalls $]1, \ p-1] \in \mathbb{Z}$ gewählt wird. Anders als beim Fermat-Test werden beim Miller-Rabin-Test mehrere Basen $n$ als sogenannte Zeugen verwendet.

Eine Basis $n$ gilt als Belastungszeuge für $p$ , wenn $n^2 \ mod \ p=1$ ist, aber $n \neq 1$ und $n \neq p-1$ .
Die Begründung hierfür ist folgende:

Ist $p$ eine Primzahl, dann ist $\mathbb{Z}_p$ ein Körper. In einem mathematischen Körper hat jede quadratische Gleichung höchstens zwei unterschiedliche Lösungen. Nun hat aber in $\mathbb{Z}_p$ die quadratische Gleichung $n^2=1$ schon die beiden Lösungen $n=1$ und $n=-1=p-1$ . Da $p>2$ vorausgesetzt werden kann, sind diese auch verschieden. Gibt es nun noch eine weitere Lösung, dann kann $\mathbb{Z}_p$ kein Körper sein. Dann kann auch $p$ keine Primzahl sein.

Beispiel:
Vermutete Primzahl $p=37 \longrightarrow p-1=36=b_i$
Ausgehend vom Satz von Fermat: $n^{p-1} \ mod \ p=1$
$p-1$ wird solange durch zwei dividiert bis ein ungerader Wert $b_1 \in \mathbb{Z}$ entsteht:
36 : 2 = 18
18 : 2 = 9
Diese Werte $b_{1...i} \in \mathbb{Z}$ werden anschleißend in eine Tabelle eingetragen und die Berechnungen $n^{b_{1...i}} \ mod \ p$ durchgeführt. Die Basis $n$ für die Exponentation liegt im Intervall $]1, \ p-1]$ .

$n$	$n^9 \ mod \ 37$	$n^{18} \ mod \ 37$	$n^{36} \ mod \ 37$
5	6	36	1
12	1	1	1
15	31	36	1

Aus den 1-sen in der letzten Spalte kann nun geschlossen werden, dass es sich bei $p=37$ mit hoher Wahrscheinlichkeit um eine Primzahl handelt.

Mit Hilfe der Programmiersprache Python, kann der Miller-Rabin-Test wie folgt beschrieben werden:

from random import randint

def millerRabin(prim):
    tmp = prim - 1
    wPrim = True
    i = 0
    while i < 20:
        basis = randNumber(tmp)
        while tmp % 2 == 0:
            if basis**tmp % prim == 1:
                wPrim = True
                break
            else:
                wPrim = False
            tmp = tmp // 2
        if not wPrim:
            break
        i += 1
    if wPrim:
        print("wahrscheinlich Primzahl.")
    else:
        print("Keine Primzahl.")
        
    
def randNumber(wert):
    return randint(2, wert)

def isgerade(zahl):
    if zahl == 2:
        print("wahrscheinlich Primzahl.")
    elif zahl % 2 == 0 and zahl > 2:
        print("Keine Primzahl.")
    else:
        if millerRabin(zahl):
            print("wahrscheinlich Primzahl.")
        else:
            print("Keine Primzahl")

if __name__ == '__main__':
    prim = 561
    isgerade(prim)

Im obigen Programm wird, anders als beim Fermat-Test, die 561 (Pseudoprimzahl) als nicht Primzahl durch den Miller-Rabin-Test erkannt. Um ein besseres Laufzeitverhalten zu gewährleisten, kann die Anzahl der Schleifendurchläufe und die Anzahl der zu testenden Basen reduziert werden. Dies geht allerdings auf Kosten der Treffergenauigkeit. Man sollte demzufolge eine gute Balance zwischen Treffergenauigkeit und Laufzeitverhalten finden.

Fermat-Test

Veröffentlicht am 20. November 2018 von juergen

Antworten

Mit Hilfe des Fermat-Tests kann mit einer gewissen Wahrscheinlichkeit ausgesagt werden, ob eine gegebene Zahl eine Primzahl ist.
Der fermatsche Primzahlttest beruht auf dem kleinen Satz von Fermat.
Für jede Primzahl $p$ und jede dazu teilerfremde natürliche Zahl $a$ ist folgende Kongruenz erfüllt:

$a^{p-1} \equiv 1 \ mod \ p$

Beispiel:
Man nehme eine zu $p$ teilerfremde natürliche Zahl, zum Beispiel 2, und bilde $2^{p-1} \ mod \ p$ .
Kommt etwas anderes als 1 heraus, so kann $p$ keine Primzahl sein. Kommt 1 heraus, so ist $p$ ziemlich wahrscheinlich eine Primzahl.
Im ersten Fall spielt die Zahl 2 die Rolle eines Belastungszeugen (engl. witness) dafür, dass $p$ zusammengesetzt ist. Im zweiten Fall kann der Zeuge 2 die Zahl $p$ nicht belasten. Somit muss $p$ mangels Beweisen freigesprochen werden. Ob $p$ aber wirklich unschuldig (= Primzahl) ist, bleibt zumindest zweifelhaft.

Der Fermat-Test kann mit Hilfe von Python wie folgt implementiert werden:

def fermat(zeuge, testzahl):
    if zeuge ** (testzahl-1) % testzahl != 1:
        print("Keine Primzahl.")
    else:
        print("wahrscheinlich Primzahl.")

if __name__ == '__main__':
    '''Pseudoprimzahl bezgl. Fermat-Test'''
    testzahl = 561 
    zeuge = 2
    fermat(zeuge, testzahl)

Das obige Phython-Programm liefert als Ergebnis für die Testzahl 561 mit Zuhilfenahme der 2 als Zeuge „wahrscheinlich Primzahl“. Die Testzahl 561 ist allerdings keine Primzahl. Sie lässt sich in die Primfaktoren 17, 11 und 3 ( $3 \cdot 11 \cdot 17 = 561$ ) zerlegen. Hierbei handelt es sich um eine sogenannte Pseudoprimzahl zur Basis 2 bezüglich des Fermat-Tests (genauer gesagt ist die 561 die kleinste Carmichael-Zahl). In der Praxis spielt daher der Fermat-Test, wegen seiner nicht ausreichenden genauen Bestimmung von Primzahlen keine oder kaum eine Rolle.
Hier finden eher Primzahltests mit einer höheren Trefferwahrscheinlichkeit Anwendung (wie z. B. der Miller-Rabin-Test).

Der Euklidische- und erweiterte Euklidische Algorithmus

Veröffentlicht am 7. November 2018 von juergen

Antworten

Der Euklidische Algorithmus

Der Euklidische Algorithmus dient dazu, den größten gemeinsamen Teiler ( $ggT$ ) zweier natürlicher Zahlen zu ermitteln. Das Ermitteln des $ggT$ findet in der Kryptographie bei vielen Kryptosystemen Anwendung.

Beispiel:
Es soll für zwei natürliche Zahlen $a=285$ und $b=33$ der $ggT(285,33)$ ermittelt werden.
Formal kann die Ausgangssituation wie folgt beschrieben werden: $a=q \cdot b + r$ ( $r$ steht hierbei für den Rest der ganzahligen Division).

Beispiel für $a=285$ und $b=33$ :
$285=8 \cdot 33 + 21$
$33=1 \cdot 21 + 12$
$21=1 \cdot 12 + 9$
$12= 1 \cdot 9 + 3$
$9= 3 \cdot \textbf{3} + 0$

In der letzten Zeile kann der $ggT(285,33)=3$ abgelesen werden (fett gedruckte 3). Die Berechnung des $ggT$ ist abgeschlossen, sobald der Rest (r) den Wert 0 angenommen hat.

Kompakter kann der $ggT(285,3)$ auch in Form einer Tabelle ermittelt werden:

a	b	r
285	33	21
33	21	12
21	12	9
12	9	3
9	3	0

Die Spalte b in der letzten Zeile liefert das Ergebnis $ggT(285,33)=3$ .

Als Python-Programm lässt sich die Ermittlung des $ggT$ wie folgt implementieren:

def ggt(a ,b):
    while b!=0:
        a ,b = b, a % b
    return a

if __name__ == '__main__':
    a = 285
    b = 33
    print("Ausgabe ggt: ", ggt(a, b))

Der erweiterte Euklidische Algorithmus

Der erweiterte Euklidische Algorithmus wird u. a. dazu verwendet lineare diophantische Gleichungen der Form $a \cdot x + b \cdot y = ggT(a,b)$ zu lösen. Vielfache des $ggT(a,b)$ sind ebenfalls lösbar und können allgemein mit $a \cdot x \cdot z + b \cdot y \cdot z=z \cdot ggT(a,b)$ für $z \in \mathbb{Z}$ beschrieben werden.

Beispiel:
Gegeben sei die lineare diophantische Gleichung:

$285 \cdot x + 81 \cdot y = 3 \\$
Zuerst wir der Euklidische Algorithmus wie zuvor durchgeführt:

$285 = 3 \cdot 81 + 42\\$
$81 = 1 \cdot 42 + 39 \\$
$42 = 1 \cdot 39 + 3 \\$
$39 = 3 \cdot 13 + 0 \\$
Die Werte werden nun in eine Tabelle übertrage. Diese Tabelle erhält neben den Spalten für $a, b$ und $r$ noch zusätzlich die Spalten für die Werte $q, x$ und $y$ . Die Spalte r spielt bei der Berechnung von $x$ und $y$ keine Rolle und kann auch weggelassen werden.

a	b	q	r	x	y
285	81	3	42	2	$-1-3 \cdot 2=-7$
81	42	1	39	-1	$1-1 \cdot (-1)=2$
42	39	1	3	1	$0-1 \cdot 1=-1$
39	13	3	0	0	$1-3 \cdot 0=1$
13	0			1	0

Hierbei gilt für die Berechnungen der Werte für die Spalten $x$ und $y$ :

in die letzte Zeile wird immer für $x=1$ und $y=0$ eingetragen und
anschließend wird sich sukzessive Zeile für Zeile nach oben gearbeit, wobei gilt:

$x=y_{alt} \ und \ y=x_{alt}-q \cdot y_{alt}$

Als Lösung für das obige Beispiel gilt demnach:
$L=\{(x,y) \ | \ \{2,-7\} \} \\$
Probe: $285 \cdot 2 + 81 \cdot (-7)=3$

In Python lassen sich die Werte für $x$ und $y$ sowie der $ggT(285,81)$ wie folgt ermitteln:

def extgcd(a, b):
    x, y, xi, yi = 1, 0, 0, 1
    while b!=0:
        q=a//b
        a, b = b, a-q*b
        y, yi = yi, y-q*yi
        x, xi = xi, x-q*xi
    return a, x, y

if __name__ == '__main__':
    print("Werte a, x, y: ", extgcd(285, 81))

Der Satz von Euler

Veröffentlicht am 18. Oktober 2018 von juergen

Antworten

Der Satz von Euler stellt eine Verallgemeinerung des „kleinen Satzes von Fermat“ auf beliebige Moduli $n \in \mathbb{N}$ dar.

Der Satz von Euler besagt folgendes:

Falls der $ggT(a,n)=1 \Longrightarrow a^{\varphi(n)} \equiv 1 \ mod \ n$

Beweis:
Es gilt: $ggT(a,n)=1$ ( $a,n$ sind teilerfremd).
1) man nehme zu $n$ teilerfremde Zahlen aus $\mathbb{Z}_n$ : $k_1,\ k_2, \ \cdot\cdot\cdot,\ k_{\varphi(n)}$
2) man multipliziere $k_1,\ \cdot\cdot\cdot, \ k_m$ mit $a$ und erhält: $ak_1, \ ak_2, \ \cdot\cdot\cdot, \ ak_{\varphi(n)} \Longrightarrow ggT(ak_i,n)=1$

Einschub Beispiel:
$n=9: \varphi(9)=6 \Longrightarrow 1,\ 2,\ 4, \ 5, \ 7, \ 8$
für $a=2$ (da 2 teilerfremd zu $n$ )

$\\ 2 \cdot 1 \ mod \ 9=\textbf{2}, \\ \ 2 \cdot 2 \ mod \ 9=\textbf{4},\\ \ 2 \cdot 4 \ mod \ 9=\textbf{8}, \\ \ 2 \cdot 5 \ mod \ 9=\textbf{1}, \\ \ 2 \cdot 7 \ mod \ 9=\textbf{5}, \\ \ 2 \cdot 8 \ mod \ 9=\textbf{7} \Longrightarrow es \ entsteht \ eine \ Permutation.$

Beweis (Fortsetzung):
3) Bilden des Produktes aller $k_i$ und aller $ak_i$ $\Longrightarrow k_1 \cdot k_2 \cdot k_3 \cdot\cdot\cdot k_{\varphi(n)} \equiv ak_1 \cdot ak_2 \cdot ak_3 \cdot\cdot\cdot ak_{\varphi(n)} \ mod \ n$
4) Nun kann abschließend durch $k_i$ geteilt werden, da alle $k_i$ teilerfremd zu $n$ sind.
$\Longrightarrow 1 \equiv a^{\varphi(n)} \ mod \ n \quad (q.e.d)$

Der Satz von Euler dient der Reduktion großer Exponenten $modulo \ n$ . Praktische Anwendung findet er u.a. in der Kryptographie beispielsweise beim RSA-Verschlüsselungsverfahren.

Der kleine und der große Satz von Fermat

Veröffentlicht am 16. Oktober 2018 von juergen

Antworten

Der kleine Satz von Fermat

Der kleine Satz von Fermat trifft folgende Aussage:
Wenn $p \in \mathbb{P}$ (also wenn $p$ eine Primzahl ist) und wenn $p \nmid a$ ( $p$ teilt nicht $a$ ) dann gilt für alle $a$ aus $\mathbb{Z}$ :

$a^{p-1} \equiv 1 \ mod \ p$

Beweis:
Seien $a,2a, \ \cdot\cdot\cdot,\ (p-1)a$ von $p-1$ verschiedene Zahlen. Dann kann gezeigt werden, dass es zu jedem $j \in \{1,\ \cdot\cdot\cdot,\ p-1 \}$ genau ein $k \in \{1, \ \cdot\cdot\cdot, \ p-1\}$ gibt, so dass

$j \cdot a \equiv k \ mod \ p$ (1)

vorliegt. Im Widerspruch zur Behauptung wird nun angenommen, dass $j \neq j'$ und $k \in \{1, \ \cdot\cdot\cdot, \ p-1\}$ vorgefunden werden kann, so dass

$j \cdot a \equiv k \equiv j' \cdot a \ mod \ p$ (2)

gilt. Da $p$ eine Primzahl und kein Teiler von $a$ ist, muss $ggT(a,p)=1$ sein. Auf Grund dessen, kann durch $a$ gekürzt werden und man erhält:

$j \equiv j' \ mod \ p$

Wegen $j,j' \in \{1, \ \cdot\cdot\cdot, \ p-1\}$ ist daher $j = j'$ im Widerspruch zu $j \neq j'$ . Die Behauptung (1) ist daher richtig.

Die jeweils zusammengehörenden Kongruenzen (1) für $j=1, \ 2, \cdot\cdot\cdot, \ (p-1)$ können nun mit $a$ erweitert werden und man erhält dann:

$1 \cdot 2 \cdot\cdot\cdot(p-1) \equiv a \cdot 2a \cdot\cdot\cdot (p-1)a \equiv a^{p-1}1 \cdot 2 \cdot\cdot\cdot (p-1) \ mod \ p$

Da $1 \cdot 2 \cdot\cdot\cdot (p-1)=(p-1)!$ und die Primzahl $p$ teilerfremd sind können diese Konkruenzen durch $(p-1)!$ dividiert werden und man erhält die obige Behauptung.

Der große Satz von Fermat

Der große Satz von Fermat wird hier nur der Vollständigkeit halber kurz vorgestellt, da wenn man vom „kleinen Satz von Fermat“ hört, man sich berechtigterweise auch die Frage stellt, ob es dann auch einen „großen Satz von Feramt“ gibt.

Der große Satz von Fermat besagt: Ist $n=\{n \in \mathbb{N} \ | \ n >2\}$ , so kann die $n-te \ Potenz$ jeder natürlichen Zahl ungleich null nicht in die Summe zweier $n-ter \ Potenzen$ natürlicher Zahlen ungleich null zerlegt werden.

Dies bedeutet formal ausgedrückt:

$a^n+b^n=c^n$

Obige Gleichung ist für positive ganze Zahlen $a, \ b, \ c, \ n$ unlösbar wenn $n$ größer als zwei ist.

Kongruenz (Zahlentheorie)

Veröffentlicht am 15. Oktober 2018 von juergen

Antworten

Laut Wikipedia sind zwei Zahlen $a$ und $b$ kongruent $modulo \ m$ , wenn sie bei der Division durch $m$ denselben Rest haben. Dies ist genau dann der Fall, wenn sie sich um ein ganzahliges Vielfaches von $m$ unterscheiden.
Stimmen die Reste nicht überein, so nennt man die Zahlen inkongruent $modulo \ m$ . Jede Kongruenz modulo einer ganzen Zahl ist eine Kongruenz auf dem Ring der ganzen Zahlen.

Verdeutlicht wird dies anhand folgender Beispiele:

$7 \equiv 19 \ mod \ 4$ ; da $7 \ mod \ 4=3$ und $19 \ mod \ 4=3$ ist.
$5 \equiv 27 \ mod \ 11$ ; da $5 \ mod \ 11 = 5$ und $27 \ mod \ 11=5$ ist.
$3 \not\equiv 23 \ mod \ 22$ ; da $3 \ mod \ 22 = 3$ und $23 \ mod \ 22 =1$ ist.

Ein einfaches Python-Programm zum bestimmen der Kongruenz zweier Zahlen $a$ und $b$ modulo $m$ für $a,b,m \in \mathbb{Z}$ kann wie folgt implementiert werden:

def isKongruent(a, b, m):
    restA = a % m
    restB = b % m
    if restA == restB:
        return True
    else:
        return False
    
if __name__ == '__main__':
    print("Sind a und b kongruent mod m?", isKongruent(7, 19, 4))

Obiges Programm liefert als Wahrheitswert True da $7 \equiv 19 \ mod \ 4$ ist.

Die Eulersche Phi-Funktion

Veröffentlicht am 11. Oktober 2018 von juergen

Antworten

Die Eulersche $\varphi$ -Funktion gibt für jede natürliche Zahl $n$ an, wie viele zu $n$ teilerfremde natürliche Zahlen es gibt, die nicht größer als $n$ sind.

Definition:

Sei $n \in \mathbb{N}$ :
Die Eulersche $\varphi$ -Funktion ist dann definiert durch:
$\varphi(n):=|\{1\leq x \leq n \ | \ ggT(x,n)=1\}|$ dabei bezeichnet $ggT(x,n)$ den größten gemeinsamen Teiler von $x,n$ .

Beispiele:

$\varphi(12)=4\Longrightarrow$ denn in der Menge $\{1 \cdot\cdot\cdot 12\}$ sind nur die Zahlen 1, 5, 7, 11 teilerfremd.
$\varphi(13)=12\Longrightarrow$ da 13 eine Primzahl ist, sind alle Zahlen die kleiner sind als 13 teilerfremd.

Es lassen sich nun folgende Aussagen treffen:

1) Für jede Primzahl $p \in \mathbb{N}$ gilt: $\varphi(p)=p-1$ .
2) Sei $p \in \mathbb{N}$ eine Primzahl und $k \in \mathbb{N}$ . Dann gilt: $\varphi(p^k)=p^k-p^{k-1}=p^k\cdot(1-\frac{1}{p})$

Beispiel zu 2):

$\varphi(12)=\varphi(2^2 \cdot 3^1) \\ =\qquad\qquad \ 2^2 \cdot (1-\frac{1}{2}) \cdot 3^1 \cdot (1-\frac{1}{3}) \\ =\qquad \qquad \ (2^2-2^{2-1})\cdot(3^1-3^{1-1}) \\ =\qquad\qquad \ 2 \cdot 2 \\ =\qquad\qquad \ 4$

In Python lässt sich die Berechnung von $\varphi(n)$ relativ einfach wie folgt implementieren:

def calcphi(phivonN):
    i = 1
    wertPhi = 0
    while i < phivonN:
        if testggT(i, phivonN) == 1:
            wertPhi += 1
        i += 1
    return wertPhi

def testggT(i, phivonN):
    while phivonN!=0:
        i ,phivonN = phivonN, i % phivonN
    return i

if __name__ == '__main__':
    phivonN = 12
    print("Phi(",phivonN,")", "= ", calcphi(phivonN))

Division mit Rest (modulo-Funktion)

Veröffentlicht am 11. Oktober 2018 von juergen

Antworten

Sowohl im Ring der ganzen Zahlen (ganze Zahlen können ohne Einschränkung addiert, subtrahiert und multipliziert werden) als auch im Polynomring über einem Körper kann stets die Division mit Rest (euklidischer Ring) durchgeführt werden.

Formaler Algorithmus:

Seien .

1) Berechne den ganzzahligen Quotienten  von  und .
2) Berechne den Rest .
3) Gebe  und  aus.

Dann gilt:  mit .

Beispiele:

$3 \ mod \ 11=3$
$-8 \ mod \ 6=-8- \lfloor \frac{-8}{6} \rfloor \cdot 6=-8-(-2) \cdot 6=-8+12=4$
$12 \ mod \ 5=2$

Primzahlen

Veröffentlicht am 9. Oktober 2018 von juergen

Antworten

Unter einer Primzahl versteht man eine von 1 verschiedene natürliche Zahl, die nur durch 1 und durch sich selbst teilbar ist.
Die Menge der Primzahlen wird in der Regel mit dem Symbol $\mathbb{P}$ bezeichnet. Mit $\mathbb{P}$ verknüpft ist die Folge $(p_n)_{n \in \mathbb{N}}$ der nach ihrer Größe geordneten Primzahlen, die man auch Primzahlfolge nennt.

Demanch gilt:

$\mathbb{P} \supset \mathbb{N} = \{p_n \ | \ n \ \in \mathbb{N} \}$

Da wir nun festgelegt haben, was eine Primzahl ist, stellt sich nun die Frage, wofür werden diese in der Kryptographie verwendet und warum haben diese einen so großen Stellenwert inne?
In der Kryptographie basieren viele Verschlüsselungsverfahren auf Primzahlen, so z.B. das RSA (Rivest-Shamir-Adleman)-Verfahren.

Beispiel einer verschlüsselten Übertragung anhand des RSA-Verfahrens:
Die Personen Alice und Bob möchten verschlüsselt kommunizieren. Zuerst möchte Bob Alice eine geheime Nachricht schicken. Um dies zu ermöglichen, trifft Alice folgende Vorbereitungen:

1) Alice wählt zufällig zwei Primzahlen  und . 
2) Sie berechnet  und . 
3) Dann wählt Sie  mit . 
4) Alice bestimmt  mit . 
5) Dann ist  der öffentliche und  der geheime Schlüssel. 
6) Die Werte  und  löscht Alice.

Bob möchte nun Alice die Nachricht $x \in \{0,...,N-1 \}$ schicken. Er geht nun wie folgt vor:

7) Bob berechnet  und schickt  an Alice. 
8) Alice berechnet .

Es stellen sich nun z.B folgende Fragen:

Wie findet man ausreichend große Primzahlen $p$ und $q$ ?
Was bedeutet die Funktion $\varphi(N) \ (Eulersche Phi-Funktion)$ ?
Wie wird die Rechenoperation $modulo$ (Division mit Rest) angewendet ?

Auf diese Fragen wird in Beiträgen in den Kategorien Zahlentheorie und Primzahltest noch näher eingegangen.

Modulare Exponentiation („schnelles Potenzieren“)

Veröffentlicht am 8. Oktober 2018 von juergen

Antworten

Die modulare Exponentiation spielt in der Kryptographie sowie zum ver- als auch zum entschlüsseln von Nachrichten eine wichtige Rolle. Beim RSA-Verfahren z.B. besteht die Chiffrierung in der Berechnung von $m^b \ mod \ n$ .

Verschiedene Möglichkeiten eine Potenzierung duchzuführen:

Eine naive Methode wäre es durch eine Reihe von Multiplikationen
$m^b \ mod \ n$ zu berechnen. Demnach wären $b-1$ Multiplikation notwendig.
Eine weitere Methode wäre das Wiederholte Quadrieren:
$m^{16} = ( ( ( a^2 ) ^2 ) ^2 ) ^2$
Ein effizienteres Potenzieren kann auch wie folgt durchgeführt werden:
$m^{26} = m^{16} \cdot m^8 \cdot m^2$
Ein gutes Rezept für ein schnelles Potenzieren ist für ein allgemeines $m^b \$ b ins Binärsystem zu überführen:
$b = b_0 \cdot 2^0 + b_1 \cdot 2^1 + ... + b_k \cdot 2^k \$
anschließend berechnet man wiederholt Quadrate von $m$ , dies erzeugt nacheinander: $m, m^2, (m^2)^2, ..., (m^2)^k \$ und multipliziert ein $(m^2)^j$ zum Endergebnis wenn $b_j = 1$ . Daraus ergibt sich eine höchste Anzahl an Multiplikationen von $2 \cdot \lceil log_2(b) \rceil$ .

Programmbeispiel der modularen Exponentiation

Es gilt z.Bsp.:
$m^{23}=m^{22} \cdot m$

daraus folgt für $m^{22}$ :
$m^{22}=(m^{11})^2$

Rekursiv kann die modularen Exponentiation wie folgt für $m^b$ mit $b \in \mathbb{N}_0$ beschrieben werden:

Eine rekursive Implementierung der obigen Rekursionsformeln mit $m=2, \ b=4, \ n=5$ in Python mit dem Rückgabewert als Ergebnis 1:

def modexp(m, b, n):
    if b == 0:
        return 1
    if b % 2==1:
        return modexp(m, b-1, n)*m % n
    else:
        return modexp(m, b//2, n)**2 % n
    
if __name__ == '__main__':
    print(modexp(2,4,5))

Eine iterative Implementierung von $m^b \ mod \ n$ in Python nach der „naiven Methode“ sieht wie folgt aus:

def modexpIt(m, b, n):
    bs=1
    while(b > 0):
        bs *= m
        b -= 1
    erg = bs % n
    return erg
    
if __name__ == '__main__':
    print(modexpIt(2,4,5))

Das obige Beispiel verdeutlicht nocheinmal, dass für die Berechnung von $m^b \ mod \ n$ b-1 Multiplikation bzw. b-1 Schleifendurchläufe notwendig sind.
Bezugnehmend auf das Laufzeitverhalten der Iterativen Implementierung zur Berechnung von $m^b \ mod \ n$ kann man somit sagen, dass diese $O(c)$ (für $c=b-1$ ) beträgt $\Longrightarrow$ lineares Laufzeitverhalten.

Binäres Potenzieren

Das binäre Potenzieren ist eine effizientere Methode für die Exponentation, als die zuvor beschriebenen Verfahren. Sie funktioniert wie folgt:

Für $a^b$ wobei $a,b \in \mathbb{Z}$ wird $b$ binär dargestellt. Für jede 1 wird nun die Operation quadrieren und multiplizieren (QM) und für jede 0 die Operation quadrieren (Q) durchgeführt. Wobei die führende 1 gestrichen werden kann, da die Binärdarstellung für $b>0$ immer mit einer 1 beginnt und damit auch die erste Anweisung mit QM, ergibt sich hierfür $1^2 \cdot a = 1$ .

Beispiel:

für $a=5$ und $b=13 \Longrightarrow 5^{13}$ .

$b_2 \ (dual) \ =1101$ die führende 1 wird nun gestrichen $\Longrightarrow$ 101. Nun werden für $a$ folgende Operationen durchgeführt:

QM $\longrightarrow$ Q $\longrightarrow$ QM

Für $a$ ergibt sich nun:

$a^2 \cdot a \longrightarrow$ QM
$(a^2 \cdot a)^2 \longrightarrow$ Q
$((a^2 \cdot a)^2)^2 \cdot a \longrightarrow$ QM

Kongret für $a=5$ erhält man:

$((5^2 \cdot 5)^2)^2 \cdot 5 = 1220703125$

In der Programmiersprache Python lässt sich das Ganze wie folgt beschreiben:

'''Umwandlung in binaer und Ergebnis als Liste zurueckliefern'''
def sammleBin(exponent):
    binListe = []
    tmpgerade = 0
    if exponent % 2 == 0:
        tmpgerade = exponent
        exponent = exponent + 1
    while exponent != 0:
        binListe.insert(0,exponent % 2)
        exponent = exponent // 2
    if tmpgerade != 0:
        binListe[len(binListe)-1] = 0
    '''erstes Element aus Liste entfernen'''
    del binListe[0]
    return binListe

'''Entsprechende Operationen durchfuehren (QM oder Q)'''
def binPotenz(basis, expo):
    binListe = sammleBin(expo).copy()
    wert = basis
    for i in range(0, len(binListe)):
        if(binListe[i] == 1):
            wert = basis * (wert**2)
        else:
            wert = wert**2
    return wert

if __name__ == '__main__':
    print("",binPotenz(5, 13))

Nähere Informationen über die Binäre Exponentiation findet man bei Wikipedia.

IT-Sicherheit

IT- und Systemsicherheit

Archiv der Kategorie: Grundlagen Kryptographie

Miller-Rabin-Test

Fermat-Test

Der Euklidische- und erweiterte Euklidische Algorithmus

Der Euklidische Algorithmus

Der erweiterte Euklidische Algorithmus

Der Satz von Euler

Der kleine und der große Satz von Fermat

Der kleine Satz von Fermat

Der große Satz von Fermat

Kongruenz (Zahlentheorie)

Die Eulersche Phi-Funktion

Division mit Rest (modulo-Funktion)

Primzahlen

Modulare Exponentiation („schnelles Potenzieren“)

Programmbeispiel der modularen Exponentiation

Binäres Potenzieren