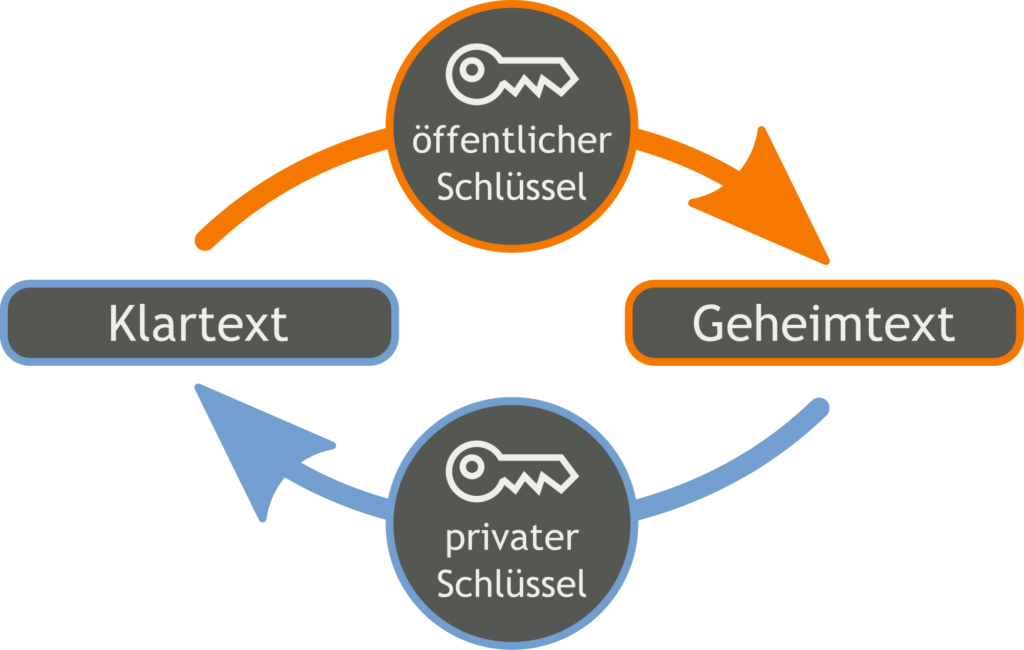
Das RSA-Verschlüsselungsverfahren gehört zu den asymmetrischen Kryptosystemen (siehe auch Beitrag symmetrische- und asymmetrische Verschlüsselung). Es wurde im Jahr 1977 von den Kryptografen Ron Rivest, Adi Shamir und Leonard Adleman entwickelt. Es eignet sich neben der eigentlichen Verschlüsselung auch als Signaturverfahren. Der RSA-Algorithmus basiert auf dem Faktorisierungsproblem.
Funktionsweise RSA
Wie schon gesagt, beruht der RSA-Algorithmus auf dem Faktorisierungsproblem. Dies besagt, dass es mathematisch sehr schwierig ist, das Produkt zweier sehr großer Primzahlen wieder in die einzelnen Faktoren in annehmbarer Zeit zu zerlegen. Aktuell ist kein Faktorisierungverfahren bekannt, das die ganzzahligen Teiler einer Zahl effizient berechnen kann. Dies hat zur Folge, dass die beiden Faktoren nur durch probieren ermittelt werden können. Dies ist bei sehr großen Primzahlen sehr aufwendig und nimmt eine wenig praktikable Zeit in Anspruch. So lange kein effizientes Verfahren zur Primfaktorenzerlegung gefunden wird, gilt das RSA-Kryptosystem als sicher.
Vorgehensweise: Es werden zwei ausreichend große Primzahlen 
und 
zufällig gewählt, die geheim bleiben müssen. Lediglich das Produkt 
ist bekannt. Anschließend konstruiert man zwei Exponenten, die in der Kryptographie als Schlüssel dienen. Einer davon ist öffentlich, der sogenannte Public Key (
), der andere privat – Private Key (
). Hierbei ist die Schlüssellänge variabel. Je länger der Schlüssel, desto sicherer ist das Verfahren.
Bei der Chiffrierung wird die zu übertragende Nachricht als Zahl 
mit dem öffentlichen Schlüssel und dem Produkt aus und zum Geheimtext 
verschlüsselt.
Zur Entschlüsselung wird benötigt:
lässt sich nicht aus berechnen, ohne die beiden Primzahlen und zu kennen.
Wichtig ist es, um es einem Angreifer unmöglich zu machen den privaten Schlüssel zu erraten, einen ausreichend großen Schlüssel zu wählen. Alle gängigen Verschlüsselungsalgorithmen sind in der Regel so konstruiert, dass die Rechenleistung moderner Computer nicht ausreichend ist, um in annehmbarer Zeit an den privaten Schlüssel durch einfaches Ausprobieren (vollständige Schlüsselsuche) zu gelangen.
Beispiel
Ein Beispiel der RSA-Verschlüsselung könnte wie folgt aussehen (der allgemeine Ablauf kann unter dem Beitrag Primzahlen nachgelesen werden):
- Wir wählen zuerst zwei Primzahlen 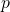und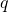
- Wert für
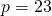
- Wert für
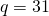
- Wert für
- Ermittlung von 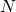mit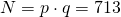
und berechne 
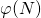mit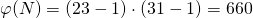 
- Wähle dann
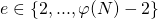mit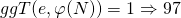 
- Bestimme 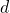mit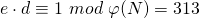
- Damit sind
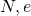der öffentliche und 
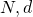der private Schlüssel 
.
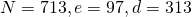Mit obigen öffentlichem Schlüssel soll nun die Zahl 5 verschlüsselt und mit dem privatem Schlüssel wieder entschlüsselt werden.
die 563 ist somit unser Geheimtext .
Der Geheimtext soll nun wieder zum Klartext entschlüsselt werden.
somit gelangen wir wieder zur 5 als Klartext .
Untenstehndes Python-Programm beschreibt im wesentlichen den RSA-Algorithmus. Auf einen Test ob und Primzahlen sind, wurde aus Gründen der Einfachheit verzichtet. Wie ein solcher Test durchgeführt wird, kann in den Beiträgen „Fermat-Test“ und „Miller-Rabin-Test“ nachgelesen werden. Weiterführende Erklärungen zu den Bestandteilen von RSA sind zu finden unter: Euklidischer- und erweiterter Euklidischer Algorithmus sowie die Eulersche Phi-Funktion.
from random import randint
'''berechnet N'''
def berechneN(p,q):
n = p * q
return n
'''berechnet phi(N)'''
def berechnePhi(p,q):
phi = (p - 1) * (q - 1)
return phi
'''berechnet den ggT(e,phi(N))'''
def berechneGGT(e,phiN):
while phiN!=0:
e ,phiN = phiN, e % phiN
return e
'''sucht ein zufaelliges e aus einer Liste'''
def sucheE(phiN):
e = 2
eListe = []
egef = False
while e <= phiN-2 and egef == False:
if berechneGGT(e, phiN) == 1:
eListe.append(e)
e = e + 1
return eListe
'''Alternative zur Ermittlung von e. Liefert erstes gefundenes e' --> schneller'''
def sucheEalter(phiN):
e = 2
eGef = e
while e <= phiN-2:
if berechneGGT(e, phiN) == 1:
eGef = e
break
e = e + 1
return eGef
'''Erweiterter Euklidischer Algorithmus zum Loesen der diophantischen Gleichung e*d+k*phi(n)=ggT(e,phi(n))=1'''
def extgcd(e, phiN):
tmpphiN = phiN
d, k, di, ki = 1, 0, 0, 1
while phiN!=0:
q=e//phiN
e, phiN = phiN, e-q*phiN
k, ki = ki, k-q*ki
d, di = di, d-q*di
if d < 0:
d = d + tmpphiN
return d
'''zufaelliges e aus Liste zurueck liefern'''
def retEtmp(laenge):
return randint(1, laenge)
'''Der Einfachheit halber, wird auf eine Pruefung, ob p und q Prim sind verzichtet --> Pruefung z.B. ueber Miller-Rabin-Test'''
if __name__ == '__main__':
p = 23
q = 31
n = berechneN(p, q)
phi = berechnePhi(p, q)
eteilerf = sucheE(phi)
laengeEListe = len(eteilerf)
randE = retEtmp(laengeEListe-1)
e = eteilerf[randE]
d = extgcd(e,phi)
print("N:", n)
print("Phi(n):", phi)
print("e (Public Key):", e)
print("d (Private Key):", d)
Sicherheit RSA
Das RSA-Kryptoverfahren beruht, wie schon erwähnt darauf, dass es schwierig ist große Primzahlen in ihre Primfaktoren zu zerlegen. Die vollständige Schlüsselsuche ist beispielsweise bei einer Schlüssellänge von 256 Bit aussichtslos. Allerdings stellt die vollständige Schlüsselsuche nicht die beste Angriffsmethode auf das RSA-Verfahren dar. Gefährlicher ist ein Faktorisierungsangriff. Dieser ist zwar sehr aufwendig, kann aber dennoch zum Erfolg führen, wenn die verwendeten Primzahlen zu klein gewählt wurden.
Im Vergleich zum AES-Verfahren bietet das RSA-Kryptosystem eine größere Angriffsfläche. Die Sicherheit von RSA hängt im wesentlichen von der Implementierung und von der gewählten Schlüssellänge ab. Ist ein Verfahren sauber programmiert, dann hat der Angreifer nur noch die Möglichkeit durch bloßes Probieren aus dem öffenlichen Schlüssel den privaten Schlüssel abzuleiten. Im wesentlichen wird eine Schlüssellänge von 2.048 Bit oder besser von 4.096 Bit empfohlen.
Ein Problem bei dem asymmetrischen Verfahren RSA ist, dass die erforderlichen Schlüssellängen für eine sichere Verschlüsselung sehr lang sind. Sollten weitere Möglichkeiten für eine schnelllere Faktorisierung ermittelt werden, so ist eine sichere Verschlüsselung mit RSA auf Grung der Länge der benötigten Schlüssel nur schwer hanhabbar. Empfehlenswert sind daher EEC (Elliptic Curve Cryptography)-Verfahren mit elliptischen Kurven. Diese kommen mit einer geringeren Schlüssellänge aus um eine hohe Sicherheit zu gewährleisten.
wobei 
geheim ist.
schnell ermittelt, da die einzelnen Werte relativ klein gewählt wurden.
. Als Ergebnis erhält man 713. Um nun die 713 wieder in ihre einzelnen Faktoren zu zerlegen, gibt es hier nur einen Weg; man muss alle Möglichkeiten durchprobieren. Sind die Primzahlen sehr groß gewählt, so dauert dies sehr sehr lange.